Tävlingsprogrammering/Uppgifter/Travar med böcker

Travar med böcker

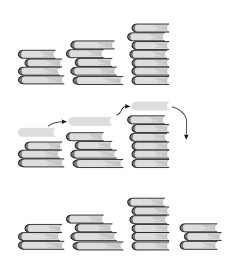
FIGUR 1. Första dagen plockas en bok från var och en av de tre travarna. Dessa tre böcker bildar en ny trave till höger om de andra.

På ett bord ligger att antal travar med böcker. Varje dag tas en bok från varje trave. Dessa böcker bildar tillsammans en ny trave till höger om de andra, se figur 1. Om en trave blir tom skjuts travarna samman från höger. Eftersom det finns ett ändligt antal böcker, kommer förr eller senare samma upplägg att återkomma. Din uppgift blir nu att skriva ett program som frågar efter första uppläggets utseende och sedan tar reda på hur lång tid det tar innan ett upplägg som tidigare funnits, återkommer.

Dag	Hög 1	Hög 2	Hög 3	Hög 4	Hög 5	Hög 6
1	4	5	7
2	3	4	6	3
3	2	3	5	2	4
4	1	2	4	1	3	5
5	1	3	2	4	6
6	2	1	3	5	5
7	1	2	4	4	5
8	1	3	3	4	5
9	2	2	3	4	5
10	1	1	2	3	4	5
11	1	2	3	4	6
12	1	2	3	5	5
13	1	2	4	4	5

I tabellen ovan visas hur antalet böcker i travarna varierar under 13 dagar. I de kommande testerna är antalet böcker ≤50, antalet travar som mest ≤15 och antalet dagar ≤100.

Körningsexempel (motsvarande tabellen ovan):

Antal travar ? 3
Böcker i trave 1 ? 4
Böcker i trave 2 ? 5
Böcker i trave 3 ? 7
Dag 13 uppkom ett upplägg, som redan förekommit dag 7

Lösning

Denna uppgift får väl räknas som en typisk simuleringsuppgift. För varje dag bör man göra två saker, först räkna ut det nya upplägget och sedan jämföra med alla tidigare upplägg och se om något av dessa är identiskt.

Det nya upplägget kan räknas ut i två steg, först ändra antalet böcker och sedan eliminera de tomma staplarna. Det kan också göras på samma gång, vilket visas i lösningen nedan.

#include <stdio.h>

int nt[15], tt[15][101],b,d,n,newn,t[15],i;

int main() {
  printf("Antal travar ? ");
  scanf("%d", &n);
  for(i=0;i<n;i++) {
    printf ("Böcker i trave %d ? ", i+1);
    scanf("%d", &t[i]);
  }
  for(d=0;d<D;d++){
    nt[d]=n;   //Lagra antalet travar den (d+1):a dagen
    for(i=0;i<n;i++) tt[d][i]=t[i];  //Lagra travarnas storlek
    for(b=0,newn=0;b<n;b++) {
      t[newn]=t[b]-1; //Plocka bort en bok från trave b, i den nya numreringen heter den newn
      if(t[newn]>0) newn++; //newn börjar skilja sig från b bara när en trave blir tom
    }
    t[newn++]=n;  //Lägg de bortplockade böckerna i en ny stapel
    n=newn; //Uppdatera antalet staplar
    //Nu ska vi kolla om upplägget förekommit tidigare
    for(b=0;b<=d;b++) if(n==nt[b]) {   //Antalet staplar måste stämma
      for(i=0;i<n;i++) if(t[i]!=tt[b][i]) break;  //Bryt loopen om en stapelstorlek inte stämmer
      if(i==n) {   //Loopen har gått färdigt: en lösning hittad
	printf("Dag %d uppkom ett upplägg, som redan förekommit dag %d\n", d+2, b+1); 
	return 0;
      }
    }
    
  }
  return 0;
}

Här är samma uppgift, fast skriven i C++ och användande standardbiblioteket (hoppas det uppskattas):

#include <vector>
#include <algorithm>
#include <iostream>

size_t min1(size_t a){return a-1;}
bool is0(size_t a){return a==0;}

int main(){
	std::vector<std::vector<size_t> > books;
	std::cout << "Antal travar ? ";
	size_t sz;
	std::cin >> sz;
	std::vector<size_t> cur(sz);
	for(size_t i=0;i<sz;++i){
		std::cout << "Böcker i trave " << i+1 << " ? ";
		std::cin >> cur[i];
	}
	cur.erase(std::remove_if(cur.begin(),cur.end(),is0),cur.end()); //Ta bort alla nollor från början
	books.push_back(cur); //Och lägg boksituationen i historiken
	while(true){
		std::transform(cur.begin(),cur.end(),cur.begin(),min1); //Minska alla med 1
		cur.push_back(cur.size()); //Lägg storleken, alltså antal böcker borttagna, längst bort i raden
		cur.erase(std::remove_if(cur.begin(),cur.end(),is0),cur.end()); //Ta bort nollor
		std::vector<std::vector<size_t> >::iterator iter=
			std::find(books.begin(),books.end(),cur); //Sök igenom historiken
		if(iter!=books.end()){ //Och om en liknande hittas, meddela användaren
			std::cout << "Dag " << books.size()+1 << 
				" uppkom ett upplägg, som redan förekommit dag " << 
				std::distance(books.begin(),iter)+1 << std::endl;
			return 0;
		}
		books.push_back(cur); //Till slut, lägger man upplägget i historiken
	}
}

Python

def ReadInput(nSize): 
    x = []
    for i in range(travar):
        x.append(input("Bocker i trave "+repr(i+1)+" ? "))
    return x

travar = input("Antal travar ? ")
travar = ReadInput(travar)
while(travar.count(0)):
    travar.remove(0)

seen = {repr(travar):1}  # Lösningen nyttjar datastrukturen dictionary
flag = True
days = 1
while(flag):
    days += 1
    for i in range(len(travar)):
        travar[i] -= 1
    travar.append(len(travar));
    while(travar.count(0)):
        travar.remove(0)
    if not repr(travar) in seen:
        seen[repr(travar)] = days
    else:
        flag = False


print "Dag "+repr(days)+" uppkom ett upplagg, som redan forekommit dag "+repr(seen[repr(travar)])

Det finns många olika sätt att lösa uppgiften på, varav alla är olika mycket omständliga. Här är ett lösningsexempel i Java som använder sig av några av de klasser som finns att tillgå. Vill man veta mer om HashMap och LinkedList, så får man kolla i Javas API. Hur som helst besparar dessa två klasser oss från en del arbete, vi kan kolla om det existerat en tidigare likadan uppsättning med bara ett metodanrop och att ta bort nollor blir enkelt med en dynamisk lista (i vårt fall en LinkedList). Att hålla på och traggla med en array går givetvis, men är oerhört drygt.

import java.util.*;

public class Travar
{
	//Metod för att ta bort alla boktravar med 0 böcker.
	public static void removeZeros(LinkedList <Integer> travar)
	{
		//Håller reda på om det finns någon nolla att ta bort.
		boolean nolla = true;

		//Så länge det finns nollar att radera kör vi.
		while(nolla)
		{
			//Tar bort en nolla och retunerar true om det fanns en.
			//Retunerar false om det inte fanns en. Anledningen till
			// att vi inte bara skrivit 0 är för att då skulle vi ta
			// bort elementet på index 0, vi vill ta bort objektet 0.
			nolla = travar.remove(new Integer("0"));
		}
	}

	public static void main(String [] klein)
	{
		Scanner scan = new Scanner(System.in);

		//Sparar hur boktravarna såg ut på en viss dag.
		//String lagrar uppsättningen boktravar, Integer lagrar dagen.
		HashMap <String, Integer> tabell = new HashMap <String, Integer> ();

		System.out.print("Antal travar: ");
		int antal = scan.nextInt();

		//Vårt bord med olika travar med böcker.
		LinkedList <Integer> books = new LinkedList <Integer> ();

		//Lagrar uppsättningen för hur boktravarna såg ut/låg denna dag.
		String boktravar = "";

		//Vilken dag det är.
		int dag = 1;

		//Läser in boktravarna.
		for(int i = 0; i<antal; i++)
		{
			System.out.print("Böcker i trave " + (i+1) + ": ");
			int book = scan.nextInt();

			//Lägger till traven med böcker på bordet.
			books.add(book);

			//Kommer ihåg hur travarna låg idag.
			boktravar += book;
		}

		//Sparar hur travarna låg på dag 1.
		tabell.put(boktravar, dag);

		//Nu ska vi gå till nästa dag.
		dag++;

		//Vi kör på tills samma upplägg kommer igen.
		while(true)
		{
			//Vår nya trave böcker som ska läggas till.
			//Eftersom man tar en bok från varje trave,
			// så kommer den ju att få samma storlek som antalet travar.
			int nyTrave = books.size();

			//Tar bort en bok från varje trave,
			for(int i = 0; i<books.size(); i++)
			{
				books.set(i, books.get(i)-1);
			}

			//Lägger till vår nya trave.
			books.add(nyTrave);

			//Tar bort alla travar med 0 böcker.
			removeZeros(books);

			//Nollställer uppsättningen.
			//Vi vill ju inte ha kvar gårdagens uppsättning.
			boktravar = "";

			//Skapar "bilden" av hur upplägget såg ut idag.
			for(int i = 0; i<books.size(); i++)
			{
				boktravar += books.get(i);
			}

			//Om vi redan har haft den här uppsättninge boktravar
			// så är vi ju klara och ska avbryta loopen.
			if(tabell.containsKey(boktravar)) break;

			//Om inte så får vi spara den här uppsättningen.
			tabell.put(boktravar, dag);

			//Vi går vidare på nästa dag.
			dag++;
		}

		//Skriver ut svaret. Eftersom vi avbryter loopen så kommer dag att visa rätt dag och boktravar
		// kommer att hänvisa oss till den dagen där den tidigare hade blivit sparad.
		System.out.println("Dag " + dag + " uppkom ett upplägg, som redan förekommit dag " + tabell.get(boktravar));
	}
}

Lösning i Haskell.

-- Travar med böcker
module Main where
import IO
import Data.Maybe
import Data.Map (Map, empty, lookup, insert)

main = do {
	putStr "Antal travar ? ";
	antal <- getLine;
	
	travar <- readTravar 1 (read antal);
	
	putStrLn $ svar travar 1 empty
}

readTravar :: Int -> Int -> IO [Int]
readTravar _ 0 = return []
readTravar n to = do {
		putStr ("Bocker i trave " ++ (show n) ++ " ? ");
		trave <- getLine;
		
		rest <- readTravar (n+1) (to-1);
		
		return $ (read trave):rest
}

svar :: [Int] -> Int -> (Map [Int] Int) -> String
svar trv n set 	| isNothing a	= svar ((filter (/= 0) (map (-1 +) trv)) ++ [length trv]) (n+1) (insert trv n set)
		| otherwise	= "Dag " ++ (show n) ++ " uppkom ett upplagg, som redan forekommit dag " ++ (show $ fromJust a)
		where
		a = Data.Map.lookup trv set

Dag	Hög 1	Hög 2	Hög 3	Hög 4	Hög 5	Hög 6
1	4	5	7
2	3	4	6	3
3	2	3	5	2	4
4	1	2	4	1	3	5
5	1	3	2	4	6
6	2	1	3	5	5
7	1	2	4	4	5
8	1	3	3	4	5
9	2	2	3	4	5
10	1	1	2	3	4	5
11	1	2	3	4	6
12	1	2	3	5	5
13	1	2	4	4	5

Dag	Hög 1	Hög 2	Hög 3	Hög 4	Hög 5	Hög 6
1	4	5	7
2	3	4	6	3
3	2	3	5	2	4
4	1	2	4	1	3	5
5	1	3	2	4	6
6	2	1	3	5	5
7	1	2	4	4	5
8	1	3	3	4	5
9	2	2	3	4	5
10	1	1	2	3	4	5
11	1	2	3	4	6
12	1	2	3	5	5
13	1	2	4	4	5

Dag	Hög 1	Hög 2	Hög 3	Hög 4	Hög 5	Hög 6
1	4	5	7
2	3	4	6	3
3	2	3	5	2	4
4	1	2	4	1	3	5
5	1	3	2	4	6
6	2	1	3	5	5
7	1	2	4	4	5
8	1	3	3	4	5
9	2	2	3	4	5
10	1	1	2	3	4	5
11	1	2	3	4	6
12	1	2	3	5	5
13	1	2	4	4	5